Paolo Mancosu
Chercheur en résidence à la Maison Suger | Mai – juin 2026


Les activités
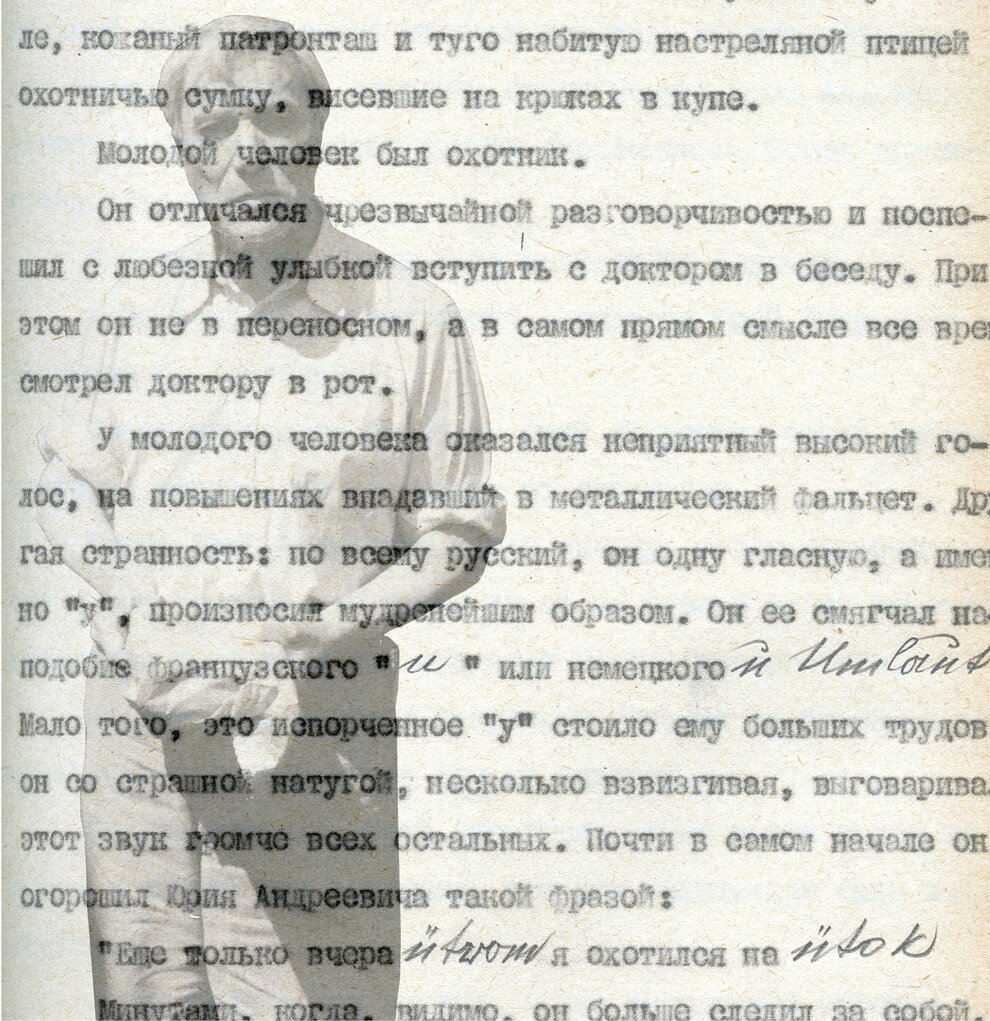
Le voyage secret du Docteur Jivago. Le roman du roman
Livres en dialogue | Soirée de présentation de l'ouvrage

Matières premières avec Paolo Mancosu
La nouvelle série de podcasts qui ouvre les portes de l'intimité des chercheuses et des chercheurs. Épisode #1

Censure et liberté intellectuelle : Boris Pasternak, le cas du Docteur Jivago
Lundi 28 février 2022 | Atelier - Maison Suger

Censure et liberté intellectuelle : Boris Pasternak, le cas du Docteur Jivago
Lundi 28 février 2022 | Atelier - Maison Suger
Publié le 4 janvier 2022








